- Última atualização: 1 de Novembro, 2024
A importância da escala: da realidade ao mapa
A escala de uma mapa é, então, o número de vezes que a realidade foi reduzida para ser representada no mapa, isto é, é a relação que existe entre a distância medida no mapa e a distância real correspondente.
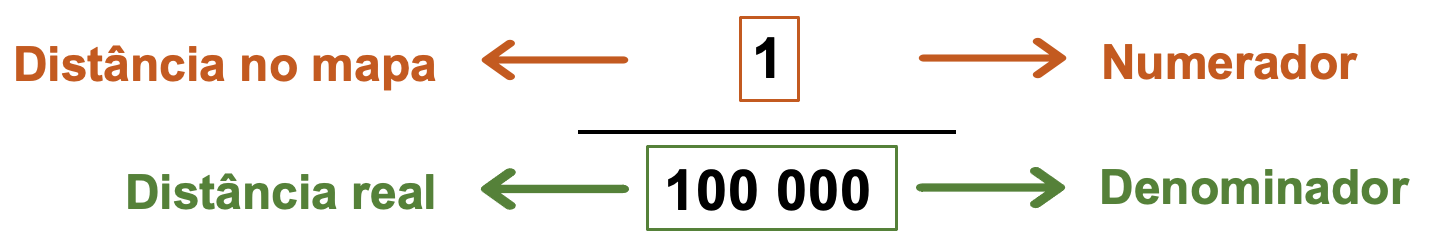
A escala numérica representada acima deve ler-se: um centímetro no mapa corresponde a 100 000 centímetros na realidade, o que significa que a realidade foi reduzida 100 000 vezes para ser representada. Assim, a realidade é 100 000 vezes maior do que está representada no mapa onde esta escala foi utilizada.
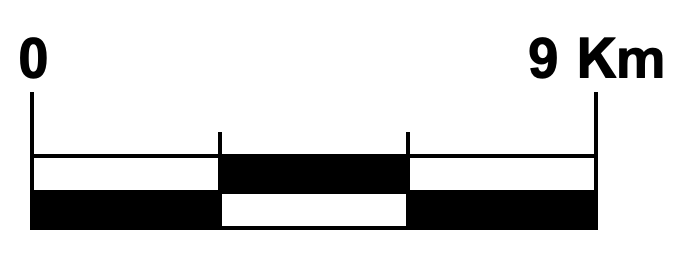
Quadro 1: Vantagens e desvantagens dos diferentes tipos de escalas.
| Tipo de escala | Principais Vantagens | Principais Desvantagens |
Escala numérica |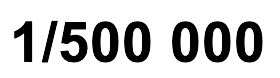
Leitura imediata do número de vezes que a realidade foi reduzida Diminui a possibilidade de existirem erros na leitura, porque implica apenas cálculos aritméticos |
Implica a realização de cálculos para determinar as distâncias reais |
Escala gráfica  |
Permite conhecer as distâncias reais de uma forma visual e simples, sem necessidade de efetuar cálculos | Aumenta a possibilidade de existirem erros na leitura, dado que implica que cada leitor faça uma medição do segmento de reta |
| Escala numérica |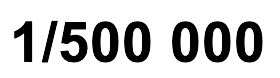
||
| Vantagens Leitura imediata do número de vezes que a realidade foi reduzida Diminui a possibilidade de existirem erros na leitura, porque implica apenas cálculos aritméticos |
||
| Desvantagens Implica a realização de cálculos para determinar as distâncias reais |
||
| Escala gráfica |
||
| Vantagens Permite conhecer as distâncias reais de uma forma visual e simples, sem necessidade de efetuar cálculos |
||
| Desvantagens Aumenta a possibilidade de existirem erros na leitura, dado que implica que cada leitor faça uma medição do segmento de reta |
O que acontece na divisão de um bolo?
Tal como acontece na divisão de um bolo, por quanto mais pessoas o bolo for dividido menor será o tamanho das fatias.
No primeiro exemplo da figura abaixo (Figura 1) vemos que um bolo foi dividido por cinco pessoas (cada fatia corresponde a 1/5 do bolo). No segundo exemplo, um bolo foi dividido por 20 pessoas (cada fatia corresponde a 1/20 do bolo). No terceiro exemplo, um bolo foi dividido por quarenta pessoas (cada fatia corresponde a 1/40 bolo). Assim, verificamos que quanto maior for o denominador ou seja o número de pessoas por quem se dividiu o bolo, menor será o tamanho das fatias do bolo, ou seja a parte do total.
Figura 1: Exemplo de escalas utilizadas em Geografia.
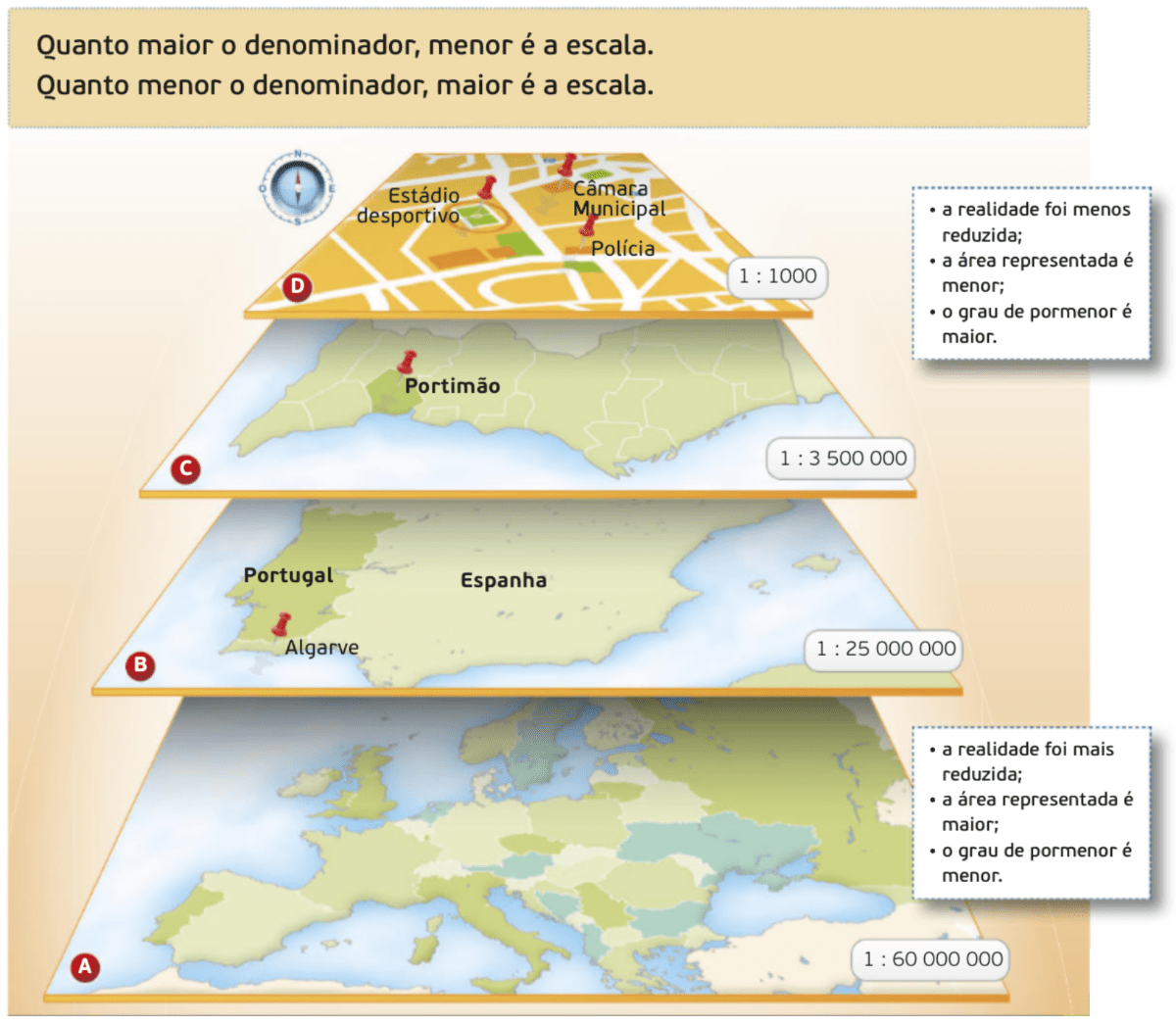
Nas escalas presentes nos mapas, quanto maior for o denominador, mais vezes a realidade foi diminuída. Assim, quanto mais a realidade é reduzida menor é a quantidade de informação representada.
Figura 2: Exemplos da variação da representação do espaço com a escala.
Figura 3: Exemplos de realidade representada a diferentes escalas.
Converter escalas numéricas para gráficas
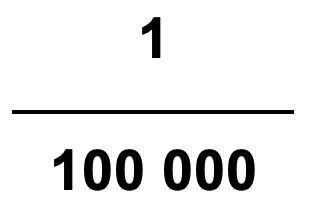
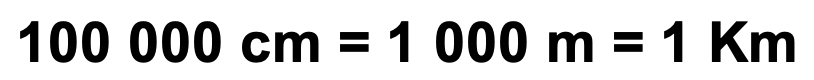2º – Desenhar um segmento de reta com um centímetro de comprimento;
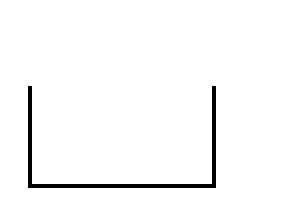3º – Atribuir o valor de zero no início e, no final do segmento de reta, o valor alcançado na conversão do denominador da escala numérica em metros ou quilómetros.
Converter escalas gráficas para numéricas
Considerando a seguinte escala: 
2º – Converter a distância real em centímetros;
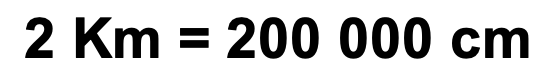3º – Apresentar a escala sob a forma de uma fração. Ao numerador deve corresponder 1 e ao denominador o valor correspondente a 1 cm do segmento de reta, convertido em centímetros.
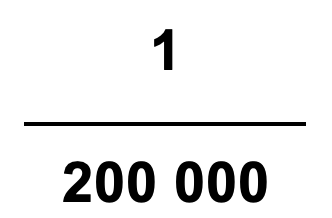
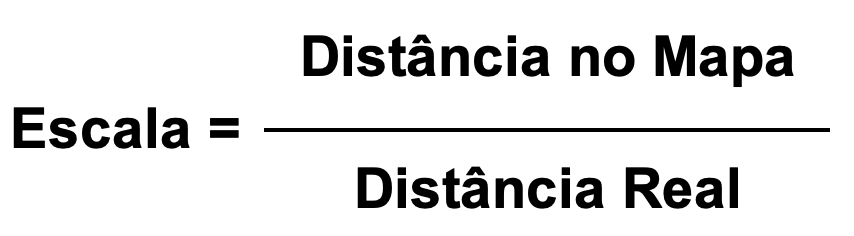
Para o cálculo de problemas com escalas devem ser apresentadas várias etapas forma a apresentar uma resposta completa. Para além das etapas seguidamente enunciadas, por vezes, é necessário um conjunto de etapas adicionais como por exemplo medir distâncias com uma régua ou fazer a conversão de números.
1º – Colocar a fórmula;
2º – Trocar a fórmula pelos valores apresentados no problema;
3º – Efetuar os cálculos;
4º – Dar uma resposta, onde deve ser explicado o resultado obtido, respeitando o enunciado.
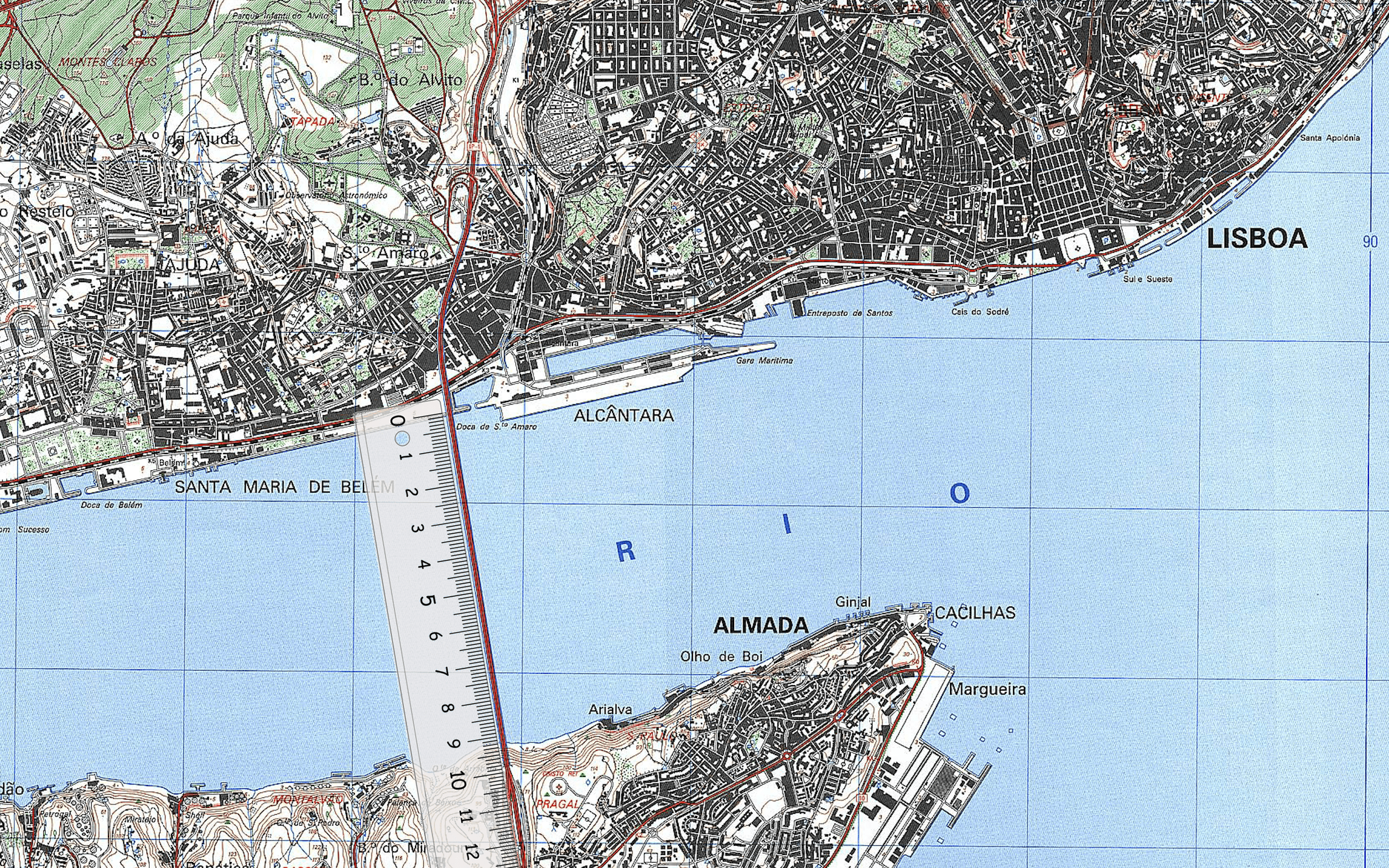
Os mapas topográficos são mapas que representam, com grande pormenor, entre outras coisas, os povoamentos ou as estradas de uma determinada área. No mapa seguinte, podemos ver um excerto da Carta Militar de Portugal nº 431 – Lisboa, publicada pelo Instituto Geográfico do Exército em 1993 (Figura 4).
Figura 4: Mapa topográfico parcial de Lisboa, folha nº 431.
Na imagem consegue-se identificar muito facilmente a Ponte 25 de Abril, sobre o Rio Tejo. Qual o seu comprimento real? Seguindo as etapas acima mencionadas, muito facilmente se consegue obter resposta para esta questão. Observa:
☞ Dados do problema:
E = 1 25 000
(todos os mapas topográficos portugueses têm esta escala)
DM = 9,1 cm
DR = ?
1º - Colocar a fórmula:
E = DM DR ⇔
2º - Trocar a fórmula por valores:
125 000 = 9,1DR ⇔
3º - Efetuar os cálculos:
DR = 25 000 x 9,11 ⇔ DR = 227 500 cm
☞ 227 500 cm = 2 275 m
4º - Dar uma resposta:
R: O comprimento da Ponte 25 de Abril (corresponde à Distância Real), entre as cidades de Lisboa e de Almada é de aproximadamente 2 275 metros.
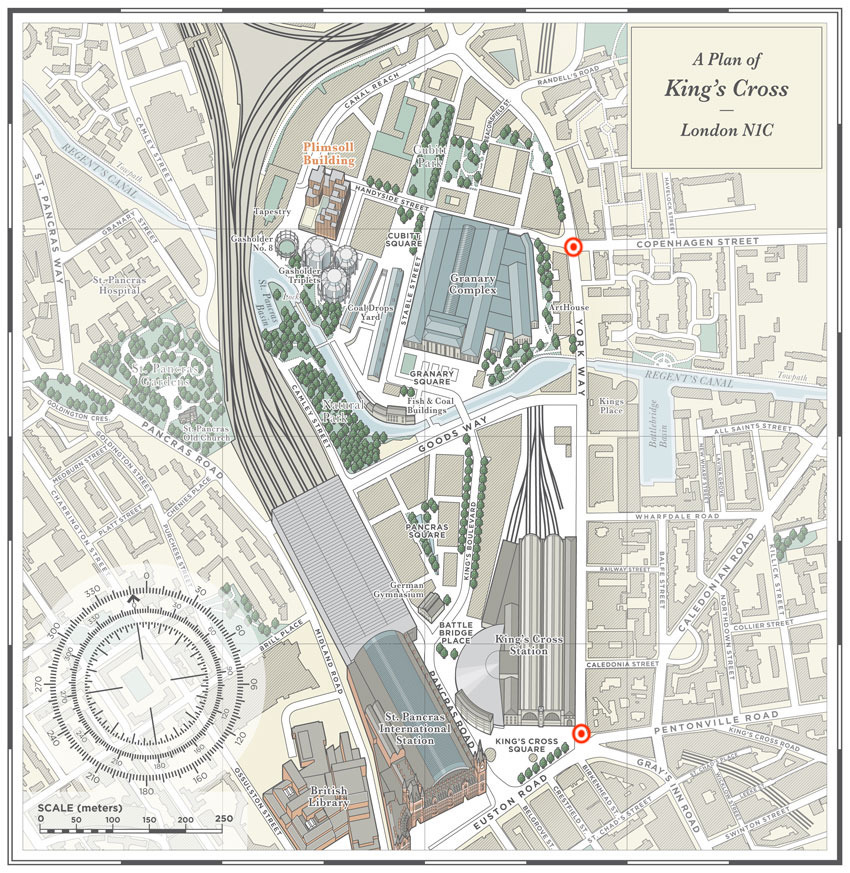
A área agora conhecida por King’s Cross, em Londres no Reino Unido (aproximadamente a 2 quilómetros a noroeste do estabelecimento romano de Londinium), ganhou este nome por ser o lugar onde antigas ruínas sugerem que possa ter existido uma travessia romana do rio Fleet e ainda pela existência de uma estátua (erguida no século XVIII, no cruzamento em frente à estação, mas já removida) do rei George IV.
Neste lugar fica também a estação de King’s Cross (onde está a famosa plataforma 9¾ dos filmes de Harry Potter), como se pode ver na figura seguinte (Figura 5).
Figura 5: Mapa parcial de King's Cross, em Londres no Reino Unido.
Na imagem consegue-se identificar muito facilmente o cruzamento de York Way e Copenhagen Street e da King’s Cross Square, assinados pelas marcas vermelhas. A que distância estão, no mapa original, estas duas marcas? Sabendo que as duas marcas estão na realidade separadas por aproximadamente 680 metros, através do uso da fórmula anterior, facilmente se consegue obter resposta para esta questão. Observa:
☞ Dados do problema:
E = 1 5 000
(na escala gráfica do mapa 1cm corresponde a 50 m ➠ 5 000 cm)
DM = ?
DR = 680 m
(680 m ➠ 68 000 cm)
1º - Colocar a fórmula:
E = DM DR ⇔
2º - Trocar a fórmula por valores:
15 000 = DM68 000 ⇔
3º - Efetuar os cálculos:
DM = 1 x 68 0005 000 ⇔ DM = 13,6 cm
4º - Dar uma resposta:
R: A distância entre os dois pontos assinalados no mapa é de aproximadamente 13,6 centímetros.
A Ponte du Gard é uma notável construção romana, construída no século I a.C., com o objetivo de ligar as duas margens do vale do rio Gard, elemento fundamental do aqueduto entre Uzès e Nîmes, em França, com aproximadamente 50 quilómetros de comprimento.
Léonce Reynaud, no seu Traité d’Architecture de 1870 representou numa planta esta notável construção, hoje Património Mundial da UNESCO (Figura 6).
Figura 6: Planta da Pont du Gard em França.
Na planta original do século XIX, a extensão do aqueduto mede 27,5 centímetros. Sabendo que na realidade mede aproximadamente 275 metros, qual a escala da planta? Observa:
☞ Dados do problema:
E = ?
(não sabemos, mas as escalas numéricas são sempre uma fração de numerador 1)
DM = 27,5 cm
DR = 275 m
(275 m ➠ 27 500 cm)
1º - Colocar a fórmula:
E = DM DR ⇔
2º - Trocar a fórmula por valores:
1E = 27,527 500 ⇔
3º - Efetuar os cálculos:
E = 1 x 27 50027,5 ⇔ E = 1 000 cm
4º - Dar uma resposta:
R: A escala da planta é de 1/1 000, ou seja, 1 centímetro na planta corresponde a 10 metros na realidade.
-
Referências
-
Bonnett, A. (2008). What is Geography? SAGE Publications Ltd.
Carta Militar de Portugal (esc.1:25,000) no 431 - Lisboa. (2006). Instituto Geográfico do Exército.
Petersen, J., Sack, D., & Gabler, R. (2015). Fundamentals of Physical Geography. Brooks/Cole Publishing Co.
Manual de leitura de Cartas. (2004). Instituto Geográfico do Exército.
Howard, P. (2011). An Introduction to Landscape. Routledge.